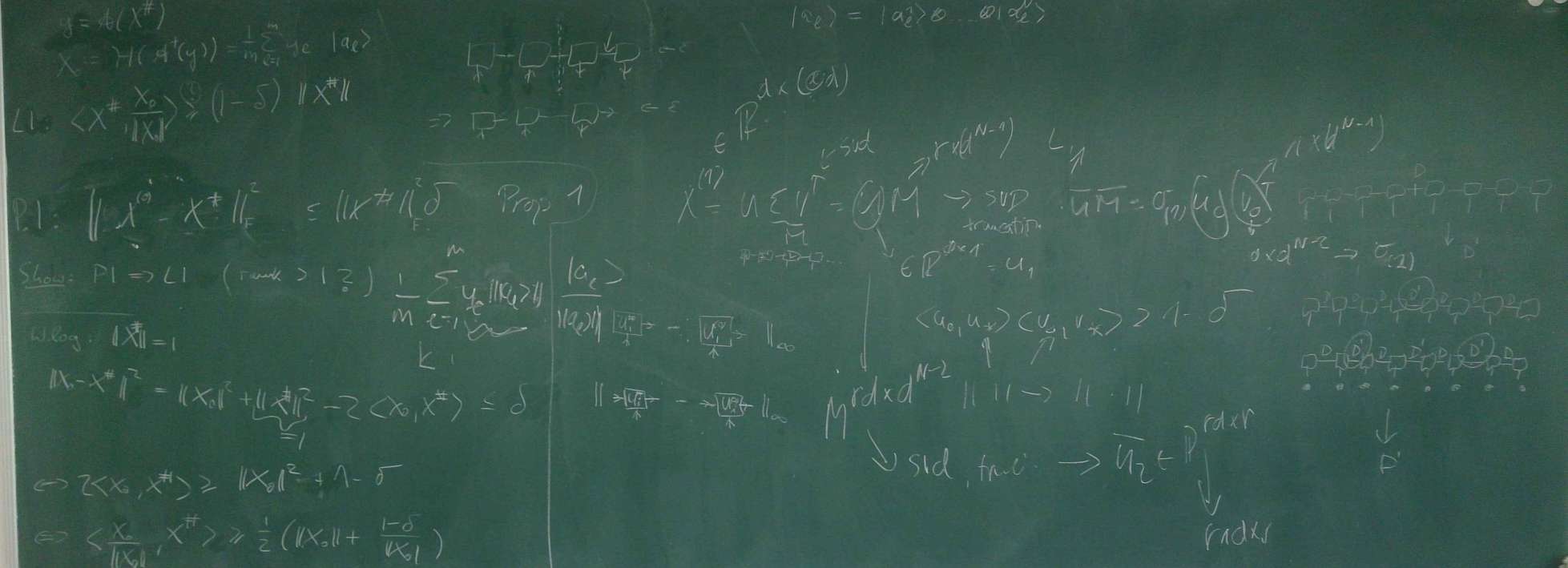 |
Topics for Master and Bachelor theses
There are good topics for theses in all research areas currently covered by the group, please ask (info@mkliesch.eu). Here is an outline of example topics.
Machine learning for quantum error correction
Quantum computers promise exponential speedups for problems that are believed to be intractable on classical computers. Currently however, operations in quantum computers are too error-prone to realize larger quantum algorithms. This problem can be appoached using quantum error correction, where quantum information is stored and processed in a redundant fashion. Quantum error correction can be greatly improved by tailoring a decoder to the noise at hand. We can estimate noise models from only the syndromes of a quantum error correction code, i.e., from the measurements that are performed for the correction process. The estimated models can then improve the error correction. For this purpose, we use powerful methods from machine learning. Possible thesis topics are the estimation of error rates on so-called quantum low-density parity check codes, the application of structure learning to estimate correlated errors or the estimation of time-dependent error rates.
Quantum tomography
Machine learning for many-body localization
In search of a quantum-mechanical mechanism for the observed break-down of transport in disordered media (such as insulators), Anderson found a single-particle description in 1958, coined Anderson localization afterwards. The natural question arising was how the mechanism could be translated to an interacting many-body case. It could be shown perturbatively that the localization can survive in the case of weak interaction or, conversely, in the case of strong disorder. In consequence, there is a phase transition between the localized phase, called the many-body localized (MBL) phase, and the delocalized phase with unsuppressed transport (as the local disorder succumbs to interactions). Despite some great effort over the recent decades, the exact mechanism of MBL is still unclear and full analytic descriptions of the phase transition are missing. Numerical efforts could probe the phases individually as well as provide phase diagrams for up to 20 particles, such as spins or fermions. Going above such system sizes is challenged by an exponentially growing Hilbert space (the number of parameters describing the system's states doubles upon adding another particle). Here, the hope is that modern machine learning techniques can be used to capture the right degrees of freedom of the MBL mechanism. This is an ongoing research endeavor with several potential topics for a thesis.